6 - Pooled prevalence for fixed pool size and tests with uncertain sensitivity and specificity

This method uses frequentist approaches to estimate prevalence and confidence limits, assuming a fixed pool size and a test with unknown (uncertain) values for sensitivity and specificity, as described below.

Method 5

This method (Method 6 from Cowling et al. (1999) assumes fixed pool size but unknown test sensitivity and specificity. Uncertainty associated with the point estimates of test sensitivity and specificity is incorporated through the inclusion of additional variance associated with the sample size used to determine the values used for these parameters. The smaller the sample size, the greater the uncertainty about the true values for sensitivity and/or specificity and hence the greater the uncertainty about the resulting prevalence estimate. Confidence limits are based on a normal approximation and may be <0 for low prevalence values.

Prevalence is estimated as for Method 3: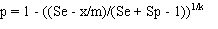

and the standard error (SE(p)) is estimated as the square root of the variance, given by: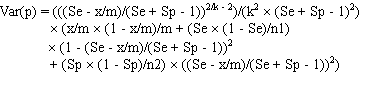

where:

• p = estimated prevalence;
• k = pool size;
• m = the number of pools tested;
• x = the number of positive pools;
• Se = the sensitivity of the test;
• Sp = the specificity of the test;
• n1 = the sample size for estimating the sensitivity of the test; and
• n2 = the sample size for estimating the specificity of the test;

Asymptotic confidence limits are calculated using the normal approximation:

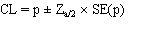
where 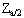is the standardised normal variate corresponding to the desired confidence limit.

Required inputs for this method are:

• pool size;
• number of pools tested;
• number of pools positive;
• assumed sensitivity of the test;
• assumed specificity of the test;
• sample sizes for estimating the sensitivity and specificity of the test; and
• desired upper and lower confidence limits for the estimate.

Pool size, number of pools, number of pools positive and sample sizes for estimating sensitivity and specificity must be positive integers and the number of positive pools must be less than the number of pools tested. Sensitivity and specificity must be >0 and <=1 and upper and lower confidence limits must be >0 and <1.

Outputs include:

• a point estimate of animal-level prevalence;
• upper and lower asymptotic confidence limits;
• the standard error for the estimate; and
• graphic and text files of estimates and confidence limits for all possible results (download by clicking on the appropriate icon).

Estimates are only valid if the proportion of positive pools is greater than the false positive rate (1 - Specificity) and less than or equal to the true positive rate (Sensitivity). Invalid results are indicated by NA in the results table.