13 - Sample size for fixed pool size and known test sensitivity and specificity

This program calculates the approximate numbers of pools required for a range of pool sizes and specified values for estimated prevalence and desired confidence and precision of the estimate, assuming fixed pool sizes and a test with known sensitivity and specificity (may be <100%). These calculations are based on a re-arrangement of the formula used to estimate asymptotic confidence limits for pooled prevalence estimates with known test sensitivity and specificity (Method 3).

The width of the asymptotic confidence intervals calculated using these sample sizes may be substantially narrower than the corresponding confidence intervals calculated using exact methods. Therefore, if exact confidence limits are to be calculated you should use the simulation option to revise sample sizes and determine the optimum sample size and pooling strategy to achieve the desired level of precision.

The required number of pools (m) to estimate the true prevalence with the desired precision is calculated as: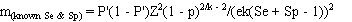

where:

• p = assumed true prevalence;
• k = pool size;
• Se = test sensitivity;
• Sp = test specificity;
• e = the acceptable error (desired precision); and
• Z = the standardised normal variate corresponding to the desired level of confidence.

and: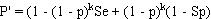

Prevalence estimates calculated from pooled testing may be upwardly biased, particularly as the probability of all pools testing positive increases (high prevalence and/or small numbers of large pools). Therefore, it is advisable to select a lower value for pool size and test a larger number of smaller pools to minimise potential bias in the result, particularly if prevalence is likely to be high. Unlike the situation with a perfect test, it is not possible to determine an optimum pool size to minimise the variance of the estimate if test sensitivity and specificity are <100%.

Required inputs for this analysis are:

• the assumed true prevalence;
• assumed test sensitivity;
• assumed test specificity;
• the desired level of precision (or acceptable error); and
• the desired level of confidence in the result.

For example, you might wish to estimate the prevalence where the true value is assumed to be about 0.01 (1%), and you wish to have 95% (0.95) confidence that the true value is within +/- 0.005 (0.5%) of your estimate, with a test that has a sensitivity of 0.9 (90%) and specificity of 0.99 (99%). The assumed prevalence, desired precision and level of confidence must all be >0 and <1. Test sensitivity and specificity must both be >0 and <=1.

You can also input a suggested pool size if desired, and the program will calculate the corresponding number of pools to be tested for that pool size (in addition to predetermined pool sizes). Suggested pool size is ignored if it is zero.

Output from the analysis is:

• the number of pools required for the input-scenario and the suggested pool size;
• a table of the numbers of pools (and total number of samples) required for the input-scenario for various pool sizes ranging from 1 to 500; and
• a graph of number of pools vs pool size.