4 - Pooled prevalence for fixed pool size and perfect tests

These methods all use frequentist approaches to estimate prevalence and confidence limits, assuming a fixed pool size and perfect (100%) test sensitivity and specificity, as described below.

Method 1

This method (Method 2 from Cowling et al. (1999) or Sacks et al. (1989) ) assumes 100% test sensitivity and specificity and fixed pool size. Confidence limits are based on a normal approximation and may be <0 for low prevalence values.

Prevalence is estimated as:

and the standard error (SE(p)) is estimated as the square root of the variance, given by: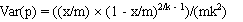

where:

• p = estimated prevalence;
• k = pool size;
• m = the number of pools tested; and
• x = the number of positive pools.

Asymptotic confidence limits are calculated using the normal approximation:

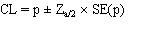
where is the standardised normal variate corresponding to the desired confidence limit.

Required inputs for this method are:

• pool size;
• number of pools tested;
• number of pools positive; and
• desired upper and lower confidence limits for the estimate.

Pool size, number of pools and number of pools positive must be positive integers and the number of positive pools must be less than the number of pools tested. Upper and lower confidence limits must be >0 and <1.

Outputs include:

• a point estimate of animal-level prevalence;
• upper and lower asymptotic confidence limits;
• the standard error for the estimate; and
• graphic and text files of estimates and confidence limits for all possible results (download by clicking on the appropriate icon).

The algorithm used to estimate prevalence and confidence limits fails if either all or none of the pools are positive. In these cases the point estimates are 100% and 0% respectively.

Method 2

This method (Method 3 from Cowling et al. (1999)) assumes 100% test sensitivity and specificity and fixed pool size. Exact confidence limits are calculated based on binomial theory, so that confidence limits are never <0 or >1.

Prevalence and variance are estimated as for Method 1:

and: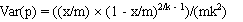

where:

• p = estimated prevalence;
• k = pool size;
• m = the number of pools tested; and
• x = the number of positive pools.

Exact confidence limits are estimated by calculating the corresponding binomial confidence limits for the proportion of positive pools and then transforming these back to individual-level prevalence values using the equation for estimating prevalence from Method 1.

Required inputs for this method are:

• pool size;
• number of pools tested;
• number of pools positive; and
• desired upper and lower confidence limits for the estimate.

Pool size, number of pools and number of pools positive must be positive integers and the number of positive pools must be less than the number of pools tested. Upper and lower confidence limits must be >0 and <1.

Outputs include:

• a point estimate of animal-level prevalence;
• upper and lower exact (binomial) confidence limits;
• the standard error for the estimate; and
• graphic and text files of estimates and confidence limits for all possible results (download by clicking on the appropriate icon).

The algorithm used to estimate prevalence and confidence limits fails if either all or none of the pools are positive. In these cases the point estimates are 100% and 0% respectively.